26. 删除有序数组中的重复项

约 2513 字大约 8 分钟

数组双指针原地算法

2025-05-17

引言

在实际开发中，我们常常需要处理数据去重的问题。特别是在处理用户输入、数据清洗或者数据预处理阶段，移除重复元素是一项基础且重要的操作。LeetCode第26题就是这样一个经典问题，它要求我们在有序数组中原地删除重复项，这不仅考察了对数组操作的基本功，还考验了我们对空间效率的把控能力。

审题

在面试中，我们首先需要明确题目的要求和约束条件：

输入是一个非严格递增排列的数组，即可能包含重复元素
需要原地删除重复元素，不能使用额外数组空间
删除后的数组应保持元素的相对顺序不变
返回值是删除重复项后数组的新长度
数组前k个位置需要包含不重复的元素，其余位置不作要求

可能的提问：

"原地删除是什么意思？" - 意味着我们需要在不使用额外数组空间的情况下完成操作
"如何处理空数组？" - 题目已明确数组长度至少为1，不存在空数组情况
"数组中的元素可以是负数吗？" - 可以，题目说明元素范围是[-10^4, 10^4]
"如何验证我的解法是否正确？" - 系统会检查返回的长度k以及数组前k个元素是否符合预期

解析

思路概述

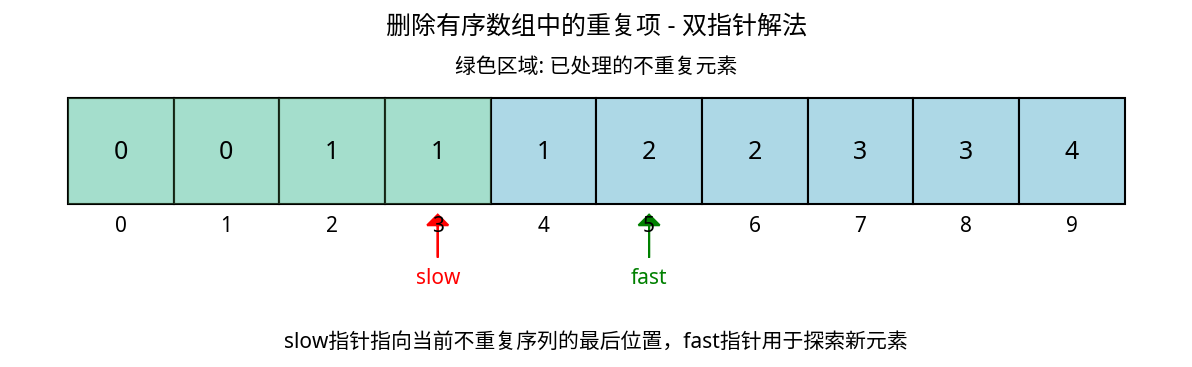
由于输入数组已经排序，相同的元素必然相邻。我们可以利用这一特性，使用双指针技巧来解决问题：

慢指针slow指向当前已处理好的不重复元素序列的最后一个位置
快指针fast用于遍历数组
当fast指向的元素与slow指向的元素不同时，说明找到了一个新的不重复元素，将slow向前移动一步，并将fast指向的元素复制到slow的新位置

算法步骤

如果数组长度为0或1，直接返回数组长度（已经没有重复元素）
初始化慢指针slow = 0，指向第一个元素
使用快指针fast从索引1开始遍历数组
比较nums[fast]和nums[slow]：
- 如果不相等，说明找到新的不重复元素，将slow加1，并将nums[fast]复制到nums[slow]
- 如果相等，说明是重复元素，只移动fast，不做其他操作
遍历结束后，slow+1就是新数组的长度（因为索引从0开始）

源码

核心代码模式

Java

class Solution {
    public int removeDuplicates(int[] nums) {
        // 处理边界情况
        if (nums.length <= 1) {
            return nums.length;
        }
        
        // 慢指针，指向当前不重复元素序列的最后一个位置
        int slow = 0;
        
        // 快指针，用于遍历数组
        for (int fast = 1; fast < nums.length; fast++) {
            // 当找到一个新的不重复元素时
            if (nums[fast] != nums[slow]) {
                // 将慢指针向前移动一步
                slow++;
                // 将新元素复制到慢指针位置
                nums[slow] = nums[fast];
            }
            // 如果是重复元素，只移动fast，不做其他操作
        }
        
        // 返回新数组的长度（索引从0开始，所以是slow+1）
        return slow + 1;
    }
}

Python

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        # 处理边界情况
        if len(nums) <= 1:
            return len(nums)
        
        # 慢指针，指向当前不重复元素序列的最后一个位置
        slow = 0
        
        # 快指针，用于遍历数组
        for fast in range(1, len(nums)):
            # 当找到一个新的不重复元素时
            if nums[fast] != nums[slow]:
                # 将慢指针向前移动一步
                slow += 1
                # 将新元素复制到慢指针位置
                nums[slow] = nums[fast]
            # 如果是重复元素，只移动fast，不做其他操作
        
        # 返回新数组的长度（索引从0开始，所以是slow+1）
        return slow + 1

JavaScript

/**
 * @param {number[]} nums
 * @return {number}
 */
var removeDuplicates = function(nums) {
    // 处理边界情况
    if (nums.length <= 1) {
        return nums.length;
    }
    
    // 慢指针，指向当前不重复元素序列的最后一个位置
    let slow = 0;
    
    // 快指针，用于遍历数组
    for (let fast = 1; fast < nums.length; fast++) {
        // 当找到一个新的不重复元素时
        if (nums[fast] !== nums[slow]) {
            // 将慢指针向前移动一步
            slow++;
            // 将新元素复制到慢指针位置
            nums[slow] = nums[fast];
        }
        // 如果是重复元素，只移动fast，不做其他操作
    }
    
    // 返回新数组的长度（索引从0开始，所以是slow+1）
    return slow + 1;
};

func removeDuplicates(nums []int) int {
    // 处理边界情况
    if len(nums) <= 1 {
        return len(nums)
    }
    
    // 慢指针，指向当前不重复元素序列的最后一个位置
    slow := 0
    
    // 快指针，用于遍历数组
    for fast := 1; fast < len(nums); fast++ {
        // 当找到一个新的不重复元素时
        if nums[fast] != nums[slow] {
            // 将慢指针向前移动一步
            slow++
            // 将新元素复制到慢指针位置
            nums[slow] = nums[fast]
        }
        // 如果是重复元素，只移动fast，不做其他操作
    }
    
    // 返回新数组的长度（索引从0开始，所以是slow+1）
    return slow + 1
}

ACM模式

Java

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        // 读取输入数组
        String line = scanner.nextLine();
        String[] strArr = line.substring(1, line.length() - 1).split(",");
        
        int[] nums = new int[strArr.length];
        for (int i = 0; i < strArr.length; i++) {
            nums[i] = Integer.parseInt(strArr[i].trim());
        }
        
        // 调用解决方案
        int k = removeDuplicates(nums);
        
        // 输出结果
        System.out.print(k + ", nums = [");
        for (int i = 0; i < k; i++) {
            System.out.print(nums[i]);
            if (i < k - 1) {
                System.out.print(",");
            }
        }
        System.out.println("]");
    }
    
    public static int removeDuplicates(int[] nums) {
        if (nums.length <= 1) {
            return nums.length;
        }
        
        int slow = 0;
        for (int fast = 1; fast < nums.length; fast++) {
            if (nums[fast] != nums[slow]) {
                slow++;
                nums[slow] = nums[fast];
            }
        }
        
        return slow + 1;
    }
}

Python

def removeDuplicates(nums):
    if len(nums) <= 1:
        return len(nums)
    
    slow = 0
    for fast in range(1, len(nums)):
        if nums[fast] != nums[slow]:
            slow += 1
            nums[slow] = nums[fast]
    
    return slow + 1

# 读取输入
line = input().strip()
nums_str = line[1:-1].split(',')
nums = [int(x.strip()) for x in nums_str]

# 调用解决方案
k = removeDuplicates(nums)

# 输出结果
result = str(k) + ", nums = ["
for i in range(k):
    result += str(nums[i])
    if i < k - 1:
        result += ","
result += "]"
print(result)

JavaScript

const readline = require('readline');
const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout
});

rl.on('line', (line) => {
    // 解析输入数组
    const numsStr = line.substring(1, line.length - 1).split(',');
    const nums = numsStr.map(s => parseInt(s.trim()));
    
    // 调用解决方案
    const k = removeDuplicates(nums);
    
    // 输出结果
    let result = k + ", nums = [";
    for (let i = 0; i < k; i++) {
        result += nums[i];
        if (i < k - 1) {
            result += ",";
        }
    }
    result += "]";
    console.log(result);
    
    rl.close();
});

function removeDuplicates(nums) {
    if (nums.length <= 1) {
        return nums.length;
    }
    
    let slow = 0;
    for (let fast = 1; fast < nums.length; fast++) {
        if (nums[fast] !== nums[slow]) {
            slow++;
            nums[slow] = nums[fast];
        }
    }
    
    return slow + 1;
}

package main

import (
    "fmt"
    "strings"
    "strconv"
)

func main() {
    // 读取输入
    var line string
    fmt.Scanln(&line)
    
    // 解析输入数组
    line = line[1:len(line)-1]
    if line == "" {
        fmt.Println("0, nums = []")
        return
    }
    
    numsStr := strings.Split(line, ",")
    nums := make([]int, len(numsStr))
    for i, s := range numsStr {
        nums[i], _ = strconv.Atoi(strings.TrimSpace(s))
    }
    
    // 调用解决方案
    k := removeDuplicates(nums)
    
    // 输出结果
    result := fmt.Sprintf("%d, nums = [", k)
    for i := 0; i < k; i++ {
        result += fmt.Sprintf("%d", nums[i])
        if i < k-1 {
            result += ","
        }
    }
    result += "]"
    fmt.Println(result)
}

func removeDuplicates(nums []int) int {
    if len(nums) <= 1 {
        return len(nums)
    }
    
    slow := 0
    for fast := 1; fast < len(nums); fast++ {
        if nums[fast] != nums[slow] {
            slow++
            nums[slow] = nums[fast]
        }
    }
    
    return slow + 1
}

吊打面试官

在面试中，面试官可能会问以下问题，我们应该如何回答：

该算法的时间复杂度和空间复杂度是多少？如何计算的？

回答：

时间复杂度：O(n)，其中n是数组的长度。我们只需要遍历一次数组，对每个元素进行常数次操作。
空间复杂度：O(1)，我们只使用了两个指针（slow和fast）作为额外空间，不随输入规模变化。这也满足了题目要求的"原地"修改数组。

该算法的核心思想是什么？

回答：这个算法的核心思想是利用双指针技巧，特别是"快慢指针"。由于数组已经排序，相同元素必然相邻，我们可以用慢指针维护不重复元素的序列，用快指针探索新的不重复元素。当快指针发现新元素时，将其复制到慢指针的下一位置，从而实现原地删除重复项的效果。

如果输入数组不是有序的，该如何调整算法？

回答：如果输入数组不是有序的，我们有几种方案：

先对数组进行排序，然后应用当前算法，时间复杂度为O(n log n)，空间复杂度取决于排序算法。

使用哈希表记录已经出现过的元素：

public int removeDuplicates(int[] nums) {
    if (nums.length <= 1) return nums.length;
    
    Set<Integer> seen = new HashSet<>();
    int index = 0;
    
    for (int num : nums) {
        if (!seen.contains(num)) {
            seen.add(num);
            nums[index++] = num;
        }
    }
    
    return index;
}

这种方法的时间复杂度是O(n)，但空间复杂度增加到O(n)，不满足原地修改的要求。

在实际面试中，我会先询问面试官是否可以使用额外空间，然后根据要求选择合适的方案。

结语

删除有序数组中的重复项是一道经典的数组处理题目，它考察了我们对数组操作的基本功和对空间效率的把控能力。通过双指针技巧，我们可以在O(n)的时间复杂度和O(1)的空间复杂度内解决这个问题。

在实际开发中，这种技巧不仅适用于数组去重，还可以应用于许多需要原地修改数组的场景，如移除特定元素、合并有序数组等。掌握这种技巧，对于提高我们处理数组问题的能力非常有帮助。

记住，当我们面对需要原地修改数组的问题时，双指针技巧往往是一个强大且高效的工具。通过合理设计指针的移动规则，我们可以在不使用额外空间的情况下，优雅地解决各种数组处理问题。

数组

哈希表

链表

动态规划