引言

大家好，我是星河！今天我们来一起探讨一道在编程面试中非常经典，也几乎是每一位程序员在学习算法时都会遇到的入门级题目——LeetCode 上的第 1 题：“两数之和”。这道题目看似简单，但它背后考察的却是我们对基础数据结构和算法效率的理解。在实际开发中，我们常常会遇到需要在数据集合中查找满足特定条件的元素对的问题，例如在电商系统中匹配商品与优惠券，或者在金融风控中识别异常交易组合等等。“两数之和”正是这类问题的简化模型，掌握它的不同解法，能为我们解决更复杂的问题打下坚实的基础。接下来，就让我们一起深入剖析这道题目吧！

题目标签

• 数据结构：数组、哈希表
• 算法类型：查找
• 难度等级：简单
• 来源平台：LeetCode

审题

在面试中，当我们遇到这道“两数之和”的题目时，千万不要急于动手写代码。我们应该像一位严谨的工程师一样，主动与面试官沟通，明确题目中的每一个细节。这不仅能帮助我们更准确地理解问题，还能展现出我们良好的沟通能力和问题分析能力。

我们可以这样向面试官提问：

1. 关于输入数组 nums：

   • “请问数组 nums 中是否可能包含重复的数字？如果包含，它们应该如何处理？” （题目已说明：你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。这意味着如果 nums = [3, 3] 且 target = 6，答案是 [0, 1]，而不是因为有两个3就产生歧义。）
   • “数组 nums 的长度范围是多少？是空的吗？还是有最小/最大长度限制？” （题目已提示：2 <= nums.length <= 10^4，所以数组至少包含两个元素，不会为空。）
   • “数组中元素的数值范围是什么？是正数、负数还是包含零？” （题目已提示：-10^9 <= nums[i] <= 10^9，这意味着元素可以是正数、负数或零。）

2. 关于目标值 target：

   • “目标值 target 的数值范围是什么？” （题目已提示：-10^9 <= target <= 10^9。）

3. 关于输出：

   • “题目要求返回的是两个整数的数组下标，请问这两个下标的顺序有要求吗？” （题目已说明：你可以按任意顺序返回答案。）
   • “如果找不到满足条件的两个数，应该如何处理？是返回一个空数组、特定的错误码，还是题目保证一定有解？” （题目已明确：只会存在一个有效答案。这意味着我们不需要处理找不到解的情况。）

4. 关于限制条件：

   • “题目中提到‘不能使用两次相同的元素’，这指的是不能使用数组中同一个位置的元素两次，对吗？例如，如果 nums = [3, 2, 4] 且 target = 6，我们不能用 nums[0] (即3) 两次来得到6，而是应该找到 nums[1] (即2) 和 nums[2] (即4)。” (是的，题目描述中“你不能使用两次相同的元素”指的就是这个意思。)

通过这些问题，我们就能够清晰地把握题目的要求：

• 输入：一个整数数组 nums (长度在 [2, 10000] 之间，元素值在 [-10^9, 10^9] 之间) 和一个整数目标值 target (值在 [-10^9, 10^9] 之间)。
• 输出：一个包含两个整数的数组，这两个整数是 nums 中和为 target 的那两个元素的下标。返回的下标顺序不限。
• 核心约束：每种输入只会对应一个答案，且同一个元素不能在结果中使用两次。

明确了这些之后，我们就可以更有信心地开始思考解题思路了。

解析

思路概述

面对“两数之和”这个问题，我们最直观的想法可能就是“暴力枚举”。也就是说，我们固定一个数，然后遍历数组中余下的其他数，看看是否有某个数与我们固定的数之和恰好等于目标值 target。这种方法简单易懂，但效率如何呢？如果数组中有 N 个元素，那么对于第一个元素，我们需要与剩下的 N-1 个元素进行比较；对于第二个元素，需要与剩下的 N-2 个元素比较，以此类推。这样算下来，总的比较次数大致是 N*(N-1)/2，时间复杂度为 O(N²)。当 N 很大的时候，这种方法的执行时间会变得非常长，显然不是最优解，尤其是在面试官追问“进阶”解法时，我们需要拿出更高效的方案。

那么，有没有更快的方法呢？我们不妨换个角度思考：当我们遍历到数组中的一个元素 nums[i] 时，我们实际上是在寻找另一个元素 nums[j] (其中 j != i)，使得 nums[i] + nums[j] = target。这个等式可以变形为 nums[j] = target - nums[i]。也就是说，对于每个 nums[i]，我们需要的“另一半” complement = target - nums[i] 是确定的。我们的任务就变成了：在数组中（不包括 nums[i] 自身）快速查找是否存在这样一个 complement。

如何才能“快速查找”呢？这正是哈希表（Hash Map 或 Dictionary）大显身手的时候了！哈希表提供了一种平均时间复杂度为 O(1) 的插入和查找操作。我们可以遍历一次数组，对于每个元素 nums[i]：

1. 首先计算出我们期望的“另一半”：complement = target - nums[i]。
2. 然后，我们去哈希表中查找这个 complement 是否已经存在。
   • 如果存在，并且这个 complement 对应的原始下标不是当前的 i（题目要求不能使用两次相同的元素，但如果数组中有重复值，例如 [3,3] target 6，哈希表中存的3和当前遍历到的3是不同位置的，是允许的），那么我们就找到了答案！返回 complement 在哈希表中存储的下标和当前元素的下标 i。
   • 如果不存在，说明到目前为止，我们还没有遇到能够与 nums[i] 配对的元素。那么，我们就将当前的 nums[i] 和它的下标 i 存入哈希表中，供后续的元素查询和配对。为什么是存 nums[i] 而不是 complement 呢？因为我们是按顺序遍历数组的，当我们遍历到 nums[k] (k > i) 时，如果 nums[k] 正好是 nums[i] 需要的 complement，那么 nums[k] 就可以在哈希表中找到之前存入的 nums[i]。

通过这种方式，我们只需要遍历数组一次，每次操作（计算、哈希表查找、哈希表插入）的平均时间复杂度都是 O(1)，所以总的时间复杂度就降到了 O(N)。当然，这是以空间换时间，因为我们额外使用了一个哈希表来存储元素及其下标，所以空间复杂度是 O(N)。在大多数情况下，这种时空权衡是非常值得的。

算法步骤

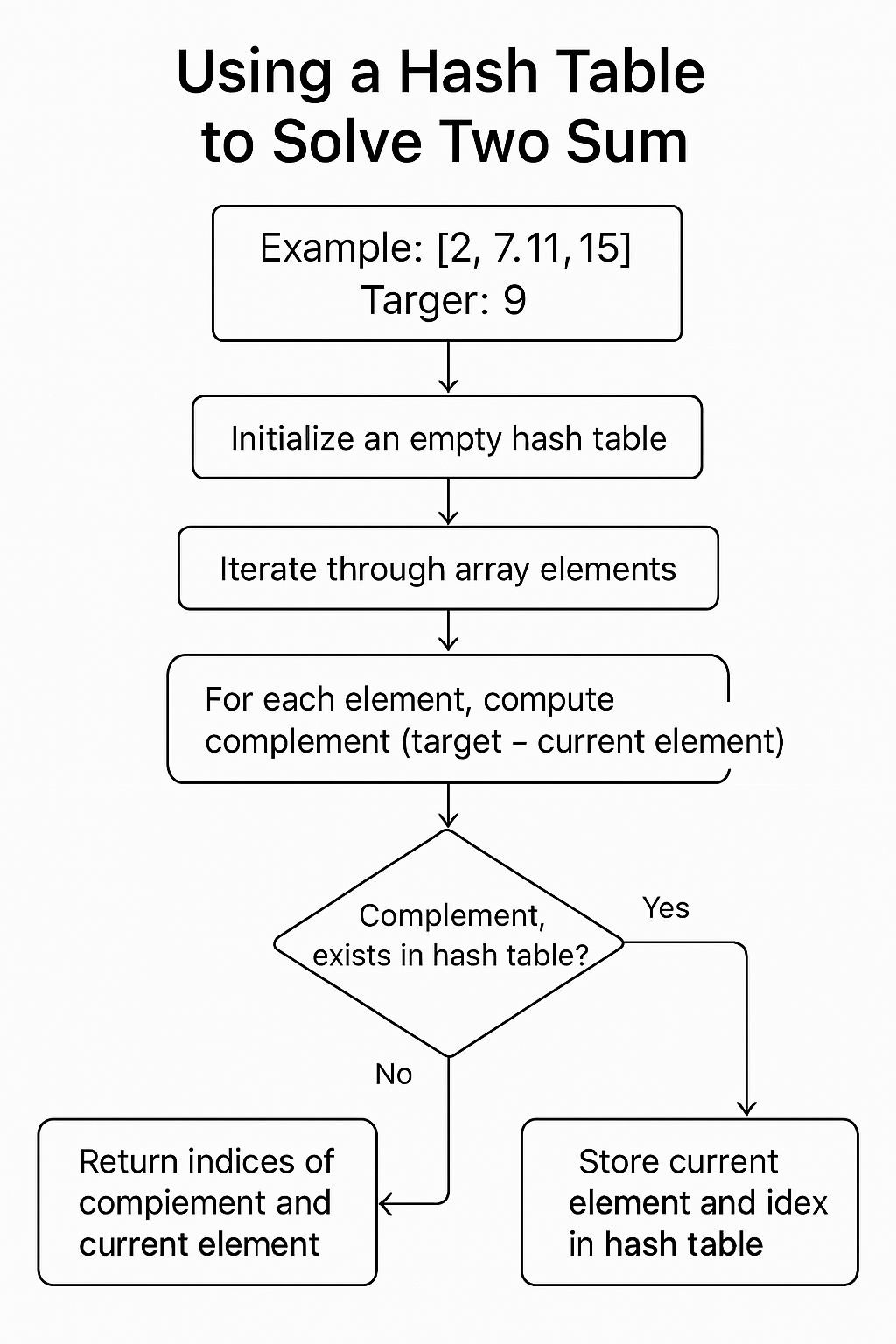
基于我们前面讨论的哈希表思路，我们可以将解题步骤归纳如下：

1. 初始化一个哈希表（HashMap/Dictionary）：我们称它为 seen_elements。这个哈希表将用来存储我们已经遍历过的数组元素及其对应的下标。键（Key）是数组元素的值，值（Value）是该元素在数组中的下标。

2. 遍历输入数组 nums：我们从数组的第一个元素开始，逐个向后遍历。对于当前遍历到的元素 nums[i]（其中 i 是当前元素的下标）：

   • 计算补数（Complement）：计算出要与 nums[i] 相加得到目标值 target 的那个数，即 complement = target - nums[i]。
   • 在哈希表中查找补数：检查 seen_elements 哈希表中是否已经存在键为 complement 的项。
     • 如果补数存在：这意味着我们在之前遍历过的元素中，找到了一个值等于 complement 的元素。假设这个补数在哈希表中对应的下标是 complement_index。那么，nums[i] 和 nums[complement_index] 就是我们要找的两个数，它们的和等于 target。此时，我们直接返回一个包含这两个下标的数组：[complement_index, i]。任务完成！
     • 如果补数不存在：这意味着到目前为止，我们还没有遇到能够与当前 nums[i] 配对形成 target 的元素。那么，我们需要将当前的元素 nums[i] 及其下标 i 存入 seen_elements 哈希表中，以备后续的元素查询。具体操作是：在 seen_elements 中添加一个新的键值对，键是 nums[i]，值是 i。

3. 遍历结束：由于题目保证“只会存在一个有效答案”，所以我们一定会在遍历过程中找到解并返回。理论上，代码不会执行到遍历完成之后还没有返回的情况。

让我们通过一个例子来模拟这个过程。假设 nums = [2, 7, 11, 15]，target = 9。

• 初始化：seen_elements = {} (空哈希表)

• i = 0, nums[0] = 2：

  • complement = 9 - 2 = 7。
  • 在 seen_elements 中查找 7，未找到。
  • 将 (2: 0) 存入 seen_elements。现在 seen_elements = {2: 0}。

• i = 1, nums[1] = 7：

  • complement = 9 - 7 = 2。
  • 在 seen_elements 中查找 2。找到了！它对应的值（下标）是 0。
  • 我们找到了解！返回 [0, 1]。

这个过程非常高效，因为哈希表的查找和插入操作平均只需要 O(1) 的时间。

源码

核心代码模式

Java

import java.util.HashMap;
import java.util.Map;

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> seenElements = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];
            if (seenElements.containsKey(complement)) {
                return new int[]{seenElements.get(complement), i};
            }
            seenElements.put(nums[i], i);
        }
        // 题目保证有解，所以这里理论上不会执行到
        return new int[]{}; 
    }
}

Python

class Solution:
    def twoSum(self, nums: list[int], target: int) -> list[int]:
        seen_elements = {}
        for i, num in enumerate(nums):
            complement = target - num
            if complement in seen_elements:
                return [seen_elements[complement], i]
            seen_elements[num] = i
        # 题目保证有解，所以这里理论上不会执行到
        return []

JavaScript

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
var twoSum = function(nums, target) {
    const seenElements = new Map();
    for (let i = 0; i < nums.length; i++) {
        const complement = target - nums[i];
        if (seenElements.has(complement)) {
            return [seenElements.get(complement), i];
        }
        seenElements.set(nums[i], i);
    }
    // 题目保证有解，所以这里理论上不会执行到
    return [];
};

Go

func twoSum(nums []int, target int) []int {
    seenElements := make(map[int]int)
    for i, num := range nums {
        complement := target - num
        if index, ok := seenElements[complement]; ok {
            return []int{index, i}
        }
        seenElements[num] = i
    }
    // 题目保证有解，所以这里理论上不会执行到
    return []int{}
}

ACM模式

Java

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        // 读取数组长度
        // LeetCode 题目通常不直接通过System.in读取长度，而是通过方法参数传递
        // 但ACM模式下，我们可能需要先读取一个n，然后读取n个数字
        // 这里我们假设输入格式是：第一行是逗号分隔的数字，第二行是target
        // 例如: 2,7,11,15
        //       9
        
        String line = scanner.nextLine();
        String[] numsStr = line.split(",");
        int[] nums = new int[numsStr.length];
        for (int i = 0; i < numsStr.length; i++) {
            nums[i] = Integer.parseInt(numsStr[i].trim());
        }
        
        int target = scanner.nextInt();
        
        Solution solution = new Solution(); // Assuming Solution class is defined as in core mode
        int[] result = solution.twoSum(nums, target);
        
        System.out.println("[" + result[0] + "," + result[1] + "]");
        scanner.close();
    }
}

// Solution class from core code mode (can be placed here or in a separate file if structured differently)
// class Solution { ... }
// For simplicity in a single file ACM submission, often the logic is directly in main or a static method.
// Below is a more typical ACM single-file structure if Solution class is not predefined.

/* 
// Alternative ACM structure if Solution class is not used separately:
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

public class Main {
    public static int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> seenElements = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];
            if (seenElements.containsKey(complement)) {
                return new int[]{seenElements.get(complement), i};
            }
            seenElements.put(nums[i], i);
        }
        return new int[]{}; // Should not be reached given problem constraints
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        String line = scanner.nextLine();
        String[] numsStr = line.split(",");
        int[] nums = new int[numsStr.length];
        for (int i = 0; i < numsStr.length; i++) {
            nums[i] = Integer.parseInt(numsStr[i].trim());
        }
        
        int target = scanner.nextInt();
        
        int[] result = twoSum(nums, target);
        
        System.out.println("[" + result[0] + "," + result[1] + "]");
        scanner.close();
    }
}
*/

Python

import sys

def solve():
    nums_str = sys.stdin.readline().strip()
    target = int(sys.stdin.readline().strip())
    
    nums = [int(x) for x in nums_str.split(",")]
    
    seen_elements = {}
    for i, num in enumerate(nums):
        complement = target - num
        if complement in seen_elements:
            print(f"[{seen_elements[complement]},{i}]")
            return
        seen_elements[num] = i

if __name__ == "__main__":
    solve()

JavaScript

// 在Node.js环境下运行ACM模式的JavaScript代码
const readline = require('readline');

const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout
});

let inputLines = [];

rl.on('line', (line) => {
    inputLines.push(line);
    if (inputLines.length === 2) { // 假设输入总是两行：数组和目标值
        const numsStr = inputLines[0];
        const target = parseInt(inputLines[1], 10);
        const nums = numsStr.split(',').map(num => parseInt(num.trim(), 10));
        
        const result = twoSum(nums, target);
        console.log(`[${result[0]},${result[1]}]`);
        rl.close();
    }
});

function twoSum(nums, target) {
    const seenElements = new Map();
    for (let i = 0; i < nums.length; i++) {
        const complement = target - nums[i];
        if (seenElements.has(complement)) {
            return [seenElements.get(complement), i];
        }
        seenElements.set(nums[i], i);
    }
    return []; // 题目保证有解
}

Go

package main

import (
	"bufio"
	"fmt"
	"os"
	"strconv"
	"strings"
)

func twoSum(nums []int, target int) []int {
	seenElements := make(map[int]int)
	for i, num := range nums {
		complement := target - num
		if index, ok := seenElements[complement]; ok {
			return []int{index, i}
		}
		seenElements[num] = i
	}
	return []int{} // 题目保证有解
}

func main() {
	scanner := bufio.NewScanner(os.Stdin)

	// 读取第一行：逗号分隔的数字字符串
	scanner.Scan()
	numsStr := scanner.Text()

	// 读取第二行：目标值
	scanner.Scan()
	targetStr := scanner.Text()
	target, _ := strconv.Atoi(strings.TrimSpace(targetStr))

	numStrSlice := strings.Split(numsStr, ",")
	nums := make([]int, len(numStrSlice))
	for i, s := range numStrSlice {
		num, _ := strconv.Atoi(strings.TrimSpace(s))
		nums[i] = num
	}

	result := twoSum(nums, target)
	fmt.Printf("[%d,%d]\n", result[0], result[1])
}

吊打面试官

当我们自信地给出哈希表解法后，面试官往往不会就此罢休，他们可能会进一步考察我们对算法的理解深度和广度。准备好迎接这些挑战了吗？我们一起来看看面试官可能会追问哪些问题，以及如何优雅地应对：

• 面试官：“你这个哈希表解法的时间复杂度和空间复杂度分别是多少？能具体解释一下是如何计算出来的吗？”

  • 我们：“好的，面试官。我使用哈希表的解法，时间复杂度是 O(N)，空间复杂度也是 O(N)，其中 N 是输入数组 nums 的长度。
    • 时间复杂度 O(N)：这是因为我们只需要遍历一次数组。在遍历过程中，对于每个元素，我们执行的操作主要包括：计算补数（O(1)）、在哈希表中查找补数（平均情况下 O(1)）、以及将当前元素及其下标存入哈希表（平均情况下 O(1)）。由于这些操作都是常数时间复杂度的，并且我们对数组中的 N 个元素都执行一次，所以总的时间复杂度是 N * O(1) = O(N)。
    • 空间复杂度 O(N)：这是因为在最坏的情况下，我们可能需要将数组中的所有 N 个元素都存入哈希表中。例如，如果数组中没有重复元素，并且直到最后一个元素才找到配对，那么哈希表会存储前 N-1 个元素。因此，哈希表占用的额外空间与输入数组的规模 N 成正比，所以空间复杂度是 O(N)。"

• 面试官：“这个算法的核心思想是什么？”

  • 我们：“这个算法的核心思想是‘空间换时间’。我们通过使用一个哈希表作为辅助数据结构，将查找“配对元素”的时间从暴力枚举的 O(N) 降低到了平均 O(1)。具体来说，就是每当我们处理一个元素时，我们不再是向后查找它的配对，而是反过来思考：‘我需要的那个配对元素之前出现过吗？’哈希表能够高效地回答这个问题。”

• 面试官：“为什么选择哈希表这种数据结构，而不是其他比如排序后双指针的方法？”

  • 我们：“这是一个很好的问题！确实，排序后使用双指针也是解决这类“两数之和”问题的常见思路。那种方法的时间复杂度是 O(N log N)（主要瓶颈在于排序），空间复杂度通常是 O(1)（如果允许修改原数组）或者 O(N)（如果不允许修改原数组，需要拷贝一份）。 我选择哈希表的原因是，题目并没有对空间复杂度做严格限制，而哈希表可以将时间复杂度优化到 O(N)，这通常比 O(N log N) 更优。此外，哈希表解法不需要改变原数组的顺序，可以直接返回原始下标，而排序双指针法如果需要返回原始下标，则需要额外处理（例如，存储原始下标再排序，或者先找到值再回头找原始下标，会增加实现的复杂度）。考虑到这些，哈希表是一个在时间和实现简洁性上都很有吸引力的选择。”

• 面试官：“如果输入数据规模非常非常大，比如内存都快放不下哈希表了，你的算法会有什么问题？有什么可以改进的思路吗？”

  • 我们：“如果数据规模大到哈希表无法完全存入内存，那么 O(N) 的空间复杂度的确会成为瓶颈。这种情况下，我们可能需要考虑：
    1. 分块处理/外部存储：如果数据可以分块读入内存，我们可以尝试对每一块数据应用哈希表方法，但这需要更复杂的逻辑来处理跨块的配对。
    2. 牺牲时间换空间：回到排序双指针的方法。虽然时间复杂度是 O(N log N)，但如果空间是首要制约因素，这会是更好的选择。如果连排序所需的额外空间（某些排序算法）都无法满足，可能就需要更特殊的外部排序算法。
    3. 近似算法或概率数据结构：如果业务场景允许一定的错误率或者只需要找到近似解，可以考虑布隆过滤器等概率数据结构来减少空间占用，但这不适用于本题这种要求精确解的场景。 对于本题的约束（nums.length <= 10^4），O(N) 的空间通常是可以接受的。”

• 面试官：“题目中说‘你可以假设每种输入只会对应一个答案’。如果这个假设不成立，也就是说，可能有多组解，或者没有解，你的算法需要做哪些调整？”

  • 我们：“如果可能有多组解，并且题目要求返回所有解：我的当前算法在找到第一组解时就会返回。如果需要所有解，我可以在找到一组解后，不立即返回，而是将这组解存起来（例如存入一个结果列表），然后继续遍历，直到整个数组遍历完毕。需要注意的是，为了避免重复记录相同的下标对（例如 [0,1] 和 [1,0] 如果被视为相同），可能需要对结果进行规范化处理（比如总是按下标小的在前）。 如果可能没有解：我的当前算法在遍历完整个数组后，如果哈希表中没有找到配对，会执行到函数末尾。目前代码是直接返回一个空数组（或根据语言特性抛出异常），这正好符合没有解的情况下的预期行为。所以，对于无解的情况，当前算法不需要大的调整，只需确保函数末尾的返回值是符合题目对无解情况的约定的即可。”

• 面试官：“如果题目要求不能使用额外的空间，即空间复杂度必须是 O(1)（不考虑输入输出占用的空间），你会怎么做？”

  • 我们：“如果空间复杂度严格限制为 O(1)，那么哈希表的方法就不适用了。这时，我会考虑：
    1. 暴力枚举：双层循环，时间复杂度 O(N²)，空间复杂度 O(1)。这是最直接的 O(1) 空间解法。
    2. 排序 + 双指针：如果允许修改输入数组（或者不考虑排序本身可能带来的空间开销，例如原地排序算法如堆排序），可以先对数组进行排序（例如 O(N log N) 时间），然后使用头尾双指针向中间逼近来查找目标和（O(N) 时间）。总时间复杂度是 O(N log N)。但这种方法会丢失原始下标，如果题目要求返回原始下标，就需要额外的处理，可能会破坏 O(1) 空间约束（例如，将 (数值, 原始下标) 对进行排序）。如果只要求返回数值，这是可行的。”

通过这样一轮深入的探讨，不仅能充分展示我们对算法的理解，还能体现出我们考虑问题的全面性和应对变化的灵活性。这才是真正“吊打”面试官的正确姿势！

结语

“两数之和”这道题目，虽然被标记为“简单”，但它就像算法世界的一扇大门，引领我们思考如何有效地从数据中提取信息。通过对暴力枚举和哈希表法的对比，我们深刻体会到了不同算法策略在效率上的巨大差异，以及“空间换时间”这一经典优化思想的威力。

更重要的是，这道题目的解题过程，从审题、构思、编码到优化、再到应对面试官的各种追问，本身就是一次完整的“解决问题”的微缩演练。它告诉我们，解决一个编程问题，不仅仅是写出能运行的代码，更要理解其背后的原理，分析其性能，并能清晰地阐述自己的思路。

希望通过星河今天的分享，大家不仅掌握了“两数之和”的解法，更能将这种分析问题、优化方案的思维方式，应用到未来遇到的更复杂的挑战中。记住，每一道看似简单的题目，都可能隐藏着值得深入挖掘的知识点。持续学习，不断精进，我们一起在算法的道路上越走越远！